The Age of the Universe and SN1987A

Introduction: An Abbreviated History of Super Nova SN1987A

• Late 20th Century: the star is noticed by the astronomer Sanduleak, and is registered in his catalog of stars in the region by its coordinates: Sk-69 202. The star is logged as blue, and spectra taken in 1977 show nothing unusual about the star. But there are important changes are taking place deep in its core, where we cannot see them with our instruments. The rings are there, but the vast distance to the system dims the rings into invisibility. The star was hot, but also may not have been hot enough to make the rings glow back then.

February 24, 1987: Sk-69 202 transforms itself into SN1987A. About 1057 ultraviolet and x-ray photons stream out from the inferno. A small fraction of this energy hits the near ring system, causing it to glow. The gas in the hourglass is not terribly dense, nor is it thick, so it glows feebly. The rings, however, are denser, and the glow is more pronounced. 50,000 parsecs away, we see three rings glowing with almost no trace of the hourglass nebula itself.

• 1990-1995: The rings fade as the gas recombines. This fading has helped us in finding the temperature, density and even the structure of the gas.
• 1996: Hubble images reveal that the supernova blast itself is measurably increasing in size. From the spectra we knew it was expanding at 5000 kilometers per second, but this was the first time such a young supernova was ever seen in such detail.
• 1997: The first true change in the ring shows up, when a spot in the north side of the ring actually begins to brighten. The hotspot becomes quite noticeable, but it is the only one seen.
• 2000: The hotspot is suddenly joined by a half dozen other spots on the opposite side of the ring. This indicates that the fastest moving pieces of the supernova are in the form of bullets of gas, and that the main front of the blast wave is slower.
• Now + a short time, maybe three to five years: The bulk of the expanding debris from the explosion, moving outwards at perhaps 10% the speed of light, slams into the inner ring. The ring starts to glow as the debris heats it up. These fireworks may be bright enough to light up the the outer rings as well. The inner ring will slow the debris somewhat, but cannot stop such an onslaught. In about twenty years, the inner ring is destroyed, obliterated by the star that once created it. Some hundreds of years later the debris hits the outer rings as well, which suffer the same fate. Their legacy remains, however: the debris fought a long time to get past the rings, and like water flowing around a sandbar, the debris itself is shaped by the rings.

Calculating the Distance to SN1987A

Where are the Rings Located?

In order to use the rings of SN1987A to trigonometrically calculate the distance, we must know where the rings lie.  Looking at the HST photo it appears rather clear that they are most likely centered about the star. The small ring is centered in the plane of the star and the two larger rings are centered at some distance from the star. In addition, if you look closely at the pixel intensity on the right figure, ring C appears to be behind all the other rings and ring A appears to be in front. Below are other observed systems which lend credence that this system is most likely of a similar configuration.

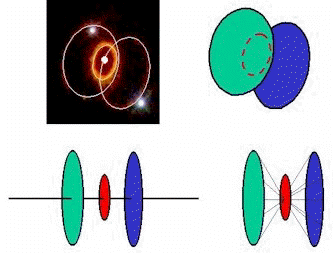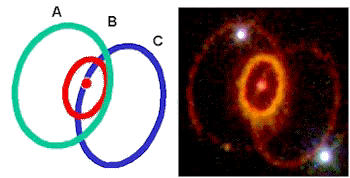There are also two other lines of evidence which make it definitive.  When SN1987A exploded, its light struck the central ring of gas after 0.658 years, illuminating it. Then, in the early 1990's it was predicted that the the expanding shock wave of matter would hit the inner ring within about 10 years making it a source of light and x-rays. This has now started to happen.  (For more details link HERE and Supernova 1987A at 10,000 days.) That the ring configuration is as indicated above is no longer in question.

Calculating the Distance to SN1987A, Todd S. Green

After the progenitor star Sk-69 202 exploded, astronomers measured the time it took for the energy to travel from the star to the primary ring that is around the star. From this, we can determined the actual radius of the ring from the star. Second, we already knew the angular size of the ring against the sky (as measured through telescopes, and measured most precisely with the Hubble Space Telescope).

So to carry out the calculation think of a right triangle as indicated in the diagram below.

• The line from SN1987A to earth (distance) is the base.
• A line from SN1987A to the ring (the radius of the ring) is the height.
• The line from the ring to earth is the hypotenuse.
• The angle between the base and the hypotenuse is half the angular size of the ring
• trig formula: base = radius ÷ tan(angle)

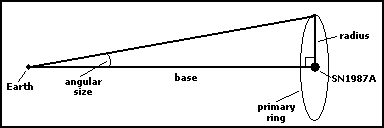
Substituting:

1. radius = 6.23 x 10¹² km (see note 1 below) = 0.658 light-years
2. angle = 0.808 arcseconds (see note 1 below) = 0.000224 degrees
3. distance = 0.658 ly ÷ tan(0.000224)
4. distance = 0.658 ly ÷ 0.00000392
5. distance = 168,000 light-years

Note that taking the measurement error limits into account makes this value 168,000 light-years ± 3.5%.

For reference:
    c (lightspeed) = 299,792.5 kilometers per second
    1 arcsecond = 1/3600°
    1 parsec = 3.26 light-years
    1 light-year ~ 9.46 x 10¹² km
    1 light-year ~ 5.88 x 10^12 miles

(The radius of the primary gas ring around SN1987A is based on the observed time it took for the energy from the explosion to hit the ring [traveling at the speed of light], which was 0.658 years [i.e., almost two-thirds of a year]. Indeed, my simple diagram of the geometry is not completely realistic, because the primary gas ring is not "flat on" perpendicular to the earth. However, rotate that ring around any way you please, and there are exactly two geometric points on the ring which represent a right triangle with the three vertexes represented by the SN1987A progenitor star, either point on the ring, and the earth, with the star and the ring point being the "height" side of the triangle and the star and the earth being the "base" side of the triangle. In actuality, the ring is tipped with respect to the earth, which means that with respect to the earth there is a "leading edge" [the closer half] and a "trailing edge" [the farther half]. Because of this fact, what astronomers observed was the point on the ring closest to the earth lighting up first [from the explosion energy] and then the rest of the gas ring progressively "light up" from the closest point to the farthest point traveling around both sides of the ring. This whole situation is described in The SN1987A Circumstellar Ring and the Distance to the Large Magellanic Cloud (A Homework Problem) by astronomer Richard McCray. Dr. McCray also has extensive discussion about the SN1987A system in his most recent paper and also at his website at: http://jilawww.colorado.edu/~dick/recent.htm )

We should take note here that SN1987A is in the Large Magellanic Cloud galaxy, which is the second closest galaxy to the earth. There are millions of other galaxies in the universe. So 168,000 years simply represents a very small lower limit. In other words, the universe must be much, much older than 168,000 years, because astronomers can literally observe events like SN1987A in these other far more distant galaxies, events that correspondingly have taken place much farther in the distant past. What makes SN1987A such a beautiful example is the presence of the primary ring, which allows a "reverse parallax" kind of direct calculation of the distance, as shown above. Thus, when you hear it said that it is a fact that the universe is ancient, this is genuinely just as factual as saying that the earth revolves around the sun. 

The Speed of Light and the Distance to SN1987A, Dave Matson

As shown above, the delayed illumination of SN1987A's ring allows a direct trigonometric calculation of the distance to that supernova.  But what if the speed of light changed over the travel time? Oddly enough, if we use the older Newtonian physics we find that a change in the speed of light does not affect our calculations of the distance to SN1987A! 

The distance is based on triangulation. The line from Earth to the supernova is one side of the triangle and the line from Earth to the edge of the ring is another leg. The third leg of this right triangle is the relatively short distance from the supernova to the edge of its ring. Since the ring lit up about a year after the supernova exploded, that means that a beam of light coming directly from the supernova reached us a year before the beam of light which was detoured via the ring. Let us assume that the distance of the ring from the supernova is really 1 unit and that light presently travels 1 unit per year.

If there had been no change in the speed of light since the supernova exploded, then the third leg of the triangle would be 1 unit in length, thus allowing the calculation of the distance by elementary trigonometry (three angles and one side are known). On the other hand, if the two light beams were originally traveling, say three units per year, the second beam would initially lag 1/3 of a year behind the first as that's how long it would take to do the ring detour. However, the distance that the second beam lags behind the first beam is the same as before. As both beams were traveling the same speed, the second beam fell behind the first by the length of the detour. Thus, by measuring the distance that the second beam lags behind the first, a distance which will not change when both light beams slow down together, we get the true distance from the supernova to its ring. The lag distance between the two beams, of course, is just their present velocity multiplied by the difference in their arrival times. With the true distance of the third leg of our triangle in hand, trigonometry gives us the correct distance from Earth to the supernova.

Consequently, supernova SN1987A is about 170,000 light-years from us (i.e. 997,800,000,000,000,000 miles) whether or not the speed of light has slowed down.

Still, the creationist has one ace of a sort remaining. Had the speed of light slowed down, as often imagined by creationists who have not advanced beyond Newtonian physics, the distance of SN1987A would still be 170,000 light-years as indicated above. However, the time that it would take for the light to reach us need not be anywhere near 170,000 years. We might counter by arguing that if the speed of light had changed then so would the decay rates of cobalt-56 and cobalt-57, and since their decay rates have been observed in SN1987A (and appear normal) that should settle it. After all, in observing SN1987A we are seeing it as it was in the past. The decay rates of cobalt-56 and cobalt-57 haven't changed, so light hasn't slowed down. (The speed of light is related to energy by E = mc^2. Thus, if the speed of light could somehow change, then energy would be affected. The end result would also be a change in the radiometric decay rates.)

Unfortunately, this argument is based on the assumption that we are observing the correct decay rates of the cobalt on SN1987A. In fact, if the speed of light had slowed down according to some reasonable curve, we would be seeing a slow motion replay of reality. The farther away objects are the greater the slow motion effect. The actual decay rates of the cobalt in SN1987A would have been much faster than what we observe today by looking at SN1987A even though we are, in effect, seeing into the past. That is, we would be seeing a slow motion replay of the decay rates of the two cobalt isotopes, and those observed rates might just happen to match the actual decay rates we observe today on earth. It would merely appear to us that no change had occurred. Does this sound confusing? If it doesn't then you are ahead of me! I'm still trying to put the pieces together!

To this one might say, "Get an education!" Relativity is central to modern science and the speed of light is a fundamental constant. Light can't go faster than about 186,000 miles a second and that's that. One could then recite volumes of laboratory studies, experiments, and observations to impress the reader with the power and reliability of special relativity. However, that approach might

seem rather dogmatic to someone lacking a good education in the sciences. Thus, I will pretend that light once traveled much faster than today (as might be imagined in Newtonian physics) and show that it still won't help the young-earth creationist.

Our first argument is based on a straightforward observation of pulsars. Pulsars put out flashes at such precise intervals and clarity that only the rotation of a small body can account for it (Chaisson and McMillan, 1993, p.498). Indeed, the more precise pulsars keep much better time than even the atomic clocks on Earth! In the mid1980s a new class of pulsars, called millisecond pulsars, were discovered which were rotating hundreds of times each second! When a pulsar, which is a neutron star smaller than Manhattan Island with a weight problem (about as heavy as our sun), spins that fast it is pretty close to flying apart. Thus, in observing these millisecond pulsars, we are not seeing a slow motion replay as that would imply an actual spin rate which would have destroyed those pulsars. We couldn't observe them spinning that fast if light was slowing down. Consequently, we can dispense with the claim that the light coming from SN1987A might have slowed down. Therefore, the decay rates observed for cobalt-56 and cobalt-57 were the actual decay rates.

A more quantitative argument can also be advanced for those who need the details. Suppose that light is slowing down according to some exponential decay curve. An exponential decay curve is one of Mother Nature's favorites. It describes radioactive decay and a host of other observations. If the speed of light were really slowing down, then an exponential decay curve would be a reasonable curve to start our investigation with. Later, we will be able to draw some general conclusions which apply to almost any curve, including those favored by creationist Barry Setterfield.

We want the light in our model to start fast enough so that the most distant objects in the universe, say 10 billion light-years away, will be visible today. That is, the light must travel 10 billion light-years in the 6000 years which creationists allow for the Earth's age. (A light year is the distance a beam of light, traveling at 186,000 miles per second, covers in one year.) Furthermore, the speed of light must decay at a rate which will reduce it to its present value after 6000 years. Upon applying these constraints to all possible exponential decay curves, and after doing a little calculus, we wind up with two nonlinear equations in two variables. After solving those equations by computer, we get the following functions for velocity and distance. The first function gives the velocity of light (light-years per year) t years after creation (t=0). The second function gives the distance (light-years) that the first beams of light have traveled since creation (since t=0).

V0 = 28,615,783 (The initial velocity for light)
K = 0.00286158 (the decay rate parameter)

With these equations in hand, it can be shown that if light is slowing down then equal intervals of time in distant space will be seen on Earth as unequal intervals of time. That's our test for determining if light has slowed down. But, where can we find a natural, reliable clock in distant space with which to do the test?

As it turns out, Mother Nature has supplied some of the best clocks around. They are the pulsars. Pulsars keep time like the Earth does, by rotating smoothly, only they do it much better because they are much smaller and vastly heavier. The heavier a spinning top is the less any outside forces can affect it. Many pulsars rotate hundreds of times per second! And they keep incredibly precise time. Thus, we can observe how long it takes a pulsar to make 100 rotations and compare that figure to another observation five years later. Thus, we can put the above creationist model to the test. Of course, in order to interpret the results properly, we need to have some idea of how much change to expect according to the above creationist model. That calculation is our next step.

Let's start by considering a pulsar which is 170,000 light-years away, which would be as far away as SN1987A. Certainly, we can see pulsars at that distance easily enough. In our creationist model, due to the initial high velocity of light, the light now arriving from our pulsar (light beam A) took about 2149.7 years to reach Earth. At the time light beam A left the pulsar it was going 487.4686 times the speed of light. The next day (24 hours after light beam A left the pulsar) light beam B leaves; it leaves at 487.4648 times the speed of light. As you can see, the velocity of light has already decayed a small amount. (I shall reserve the expression "speed of light" for the true speed of light which is about 186,000 miles per second.) Allowing for the continuing decay in velocity, we can calculate that light beam A is 1.336957 light-years ahead of light beam B. That lead distance is not going to change since both light beams will slow down together as the velocity of light decays.

When light beam A reaches the Earth, and light is now going its normal speed, that lead distance translates into 1.336957 years. Thus, the one-day interval on our pulsar, the actual time between the departures of light beams A and B, wrongly appears to us as more than a year! Upon looking at our pulsar, which is 170,000 light-years away, we are not only seeing 2149.7 years into the past but are seeing things occur 488.3 times more slowly than they really are!

Exactly 5 years after light beam A left the pulsar, light beam Y departs. It is traveling at 480.5436 times the speed of light. Twenty-four hours after its departure light beam Z leaves the pulsar. It is traveling at 480.5398 times the speed of light. Making due allowances for the continual slowing down of the light, we can calculate that light beam Y has a lead in distance over light beam Z of 1.318767 light-years. Once again, when light beam Y reached Earth, when the velocity of light had become frozen at its present value, that distance translates into years. Thus, a day on the pulsar, the one defined by light beams Y and Z, appears in slow motion to us. We see things happening 481.7 times slower than the rate at which they actually occurred.

Therefore, if the above creationist model is correct, we should see a difference in time for the above two identical intervals, a difference which amounts to about 1.3%. Of course, the above calculations could be redone with much shorter intervals without affecting the 1.3% figure, being that the perceived slowdown is essentially the same for the smaller intervals within one day. As a result, an astronomer need only measure the spin of a number of pulsars over a few years to get definitive results. Pulsars keep such accurate time that a 1.3% difference--even after hundreds of years--would stand out like a giant redwood in a Kansas wheat field!

So, what are the results of this definitive test? Many pulsars have been observed which show nothing remotely close to a 1% change in their rotation rates over a five year period. Although we have technically disproved only the above model, we have, nevertheless, thrown a monkey wrench into the machinery for decaying light speed. Every such scenario must have the slow motion effect described above. Furthermore, the slow motion effect is directly related to how fast the light is moving. If a model requires light in the past to move one hundred times faster than observed today, then, at least for some interval of time measured in that part of space, we would observe things moving one hundred times as slow.

That's the fatal point which no choice of light-velocity decay curve can wholly remedy. The creationist model, in order to be useful, must start with a high velocity for light so that objects ten billion light-years away can be seen in a universe a mere 6000 years old. Consequently, such a universe must appear, in general, to be slowing down more and more the further we look into the depths of space. And the further we look, in general, the more dramatic the perceived slowdown should be.

It might seem that if we started out with a fantastically high velocity for light, which then decayed precipitously, we could reduce the problems. Certainly, that would produce a light-velocity decay curve with near normal velocities for most of the years between t=0 and t=6000. However, the effect would be to move the departure time of light beam A (in the above model) closer to the creation time and to jack up its speed. Thus, the slow motion factor would be even worse than the model we just examined! On the other extreme, by abandoning an exponential decay curve, one can get the initial velocity down to about 1.6 million light-years per year. But alas! The velocity of light beam A is now 1.6 million light-years per year! We've gone from the frying pan into the fire.

The problem, from a graphical point of view, is that we have a certain amount of obligatory area under the velocity-time curve which must be distributed in some way. That area represents the 10 billion light-years of space which our initial light beams must cross in 6000 years. No matter where you put that area, now matter how you poke or shape it, you have a problem.

The big question, then, is whether our general observations of the universe fit such models. Do we, for example, observe pulsars spinning slower and slower the further away they are? Do the rotation of galaxies, as determined from the Doppler effect, grind to a near halt in the more remote regions of space? Do dust clouds seem to collapse more slowly the farther away they are? Do the closer novas and supernovas explode, on the whole, more quickly than the more remote ones? Do galaxies appear to be traveling any slower the farther away they are? The answer is no.

The alternative, if these light-velocity decay models are to be salvaged, is that the more distant the object the faster it is moving. Thus, we would have the illusion of seeing normal rates prevail everywhere, the slow motion factor being cancelled by objects which are moving, in truth, faster and faster the further we look into the depths of space. However, there is a limit to how fast some things can go. Millisecond pulsars are already close to flying apart. Their spin rates are no illusion! The distant galaxies, if they were really rotating millions of times faster a few thousand years ago, would have flown apart. We are led into absurdity. There is no reason, for example, for believing that the distance of a gas cloud from us dictates how fast it will collapse! We have no reason to believe that distant galaxies once traveled millions of times faster than their observed rates. Had they done so, they would surely have broken out of the great clusters of galaxies which are bound by gravity. Their distribution today would have been more or less random.

Light, itself, would have behaved differently at different speeds. The higher the speed the more blueshifted, the more energetic it would be. Certain wavelengths of light, for example, have the power to penetrate the galactic dust, thus allowing us to see events going on in the core of our galaxy. If the wavelength of such light was merely an illusion produced by the slow motion effect, if those light waves actually existed at shorter frequencies back then, they would have been absorbed or scattered differently by the galactic dust. That is to say, astronomers would not see a logical correspondence between the wavelengths they observe and their known properties. In the above example, we might not see the galactic core at all by using the preferred wavelength for dust penetration! Needless to say, astronomers don't have that problem.

Our conclusion, then, is that any model which would drive us to such views is bankrupt. We can forget about those claims that light traveled much faster in the past.

Once it's clear that the light-velocity decay models are bankrupt, not only with respect to modern science but even within Newtonian physics, then there is only one reasonable conclusion. The light coming from distant stars and galaxies have not only traveled immense distances but have spanned ages as well. In particular, the fact that supernova SN1987A is around 170,000 light-years distant means that we are seeing an event which is around 170,000 years old.

A few creationists have argued that the universe really isn't that big. In particular, Slusher, working for the Institute for Creation Research, argued in 1980 that the universe is based on a Riemannian space which allowed no point to be more than 15.71 light-years away. The great distances observed would be an illusion based on mistaking the Riemannian space for Euclidean space.

This model, however, requires that the distance to supernova SN1987A be measured at less than 15.71 light-years in contradiction to the 170,000 light-years actually measured. Unexploded versions of SN1987A would be seen at the same time, one of them being at a perceived distance of 170,000 light-years! A few decades later, the light from the explosion would circle around again, thus causing us to see SN1987A explode all over again! This is madness, not science! See Strahler (1987, pp.114-116) for a thorough debunking of this Riemannian space nonsense. (George Friedrich Bernhard Riemann, 1826-1866, was a German mathematician whose work on curved space proved helpful to Einstein, but not with the absurd radius of curvature assigned by Slusher!)

Yet another idea, advanced by Henry Morris and others, is that star light was created in situ during the Genesis creation week. However, we have now left the realm of science for theology. There is no scientific way to separate star light from its origin in a star. Not only is it theology, but it's bad theology. God creates a universe which forces him to be a deceiver! It goes beyond the need for any reasonable appearance of age as a result of functionality. There is no need, for example, to see supernovae explode before their time. An observer would ultimately see the supernova leap back together and explode all over again when the light from the real explosion finally arrived! It makes God out to be an idiot.

When the smoke blown about finally drifts away and the debate hall falls silent, the young-earth creationists find themselves back on square one. He is looking at stars many millions of light-years away, stars putting out light which takes many millions of years to reach us! Attempts to speed up the velocity of light or to shrink down the universe have come to naught. What does remain is the old age of our universe.

One final refutation from "Bayou University!"

"The study of SN 1987 A has been very exciting for astronomers and has enabled them to verify several theories about supernovae, as well as to learn surprising new information. It was not previously theorized that a blue supergiant could produce a type II supernova and the ring structure is quite unusual. But for our purposes we are interested only in the inner ring, which is now 1.37 light years in diameter. This ring was first observed about nine months after the discovery of SN 1987 A.

As expected, gamma ray emission of Co-57 and Co-56 have been detected from SN 1987 A. These gamma rays show precisely the same energy levels as Co-57 and Co-56 do on earth. This means that the speed of light at the time the gamma rays were emitted from SN 1987 A was the same as it is on earth today.

Theoretical models of a supernova predicted that the decay of Co-57 and Co-56 would cause light to be emitted by supernova gases. This light has been observed and the light curve has decayed at precisely the half-life of Co-57 and Co-56 as measured in labs on earth. Again, this means that the speed of light must necessarily be the same today as when it was emitted from SN 1987 A. The time it takes for this light to travel to the inner ring has been measured. Knowing when the supernova occurred and knowing when the ring was first observed tells us how long it takes light to travel to from the star to the ring. Given this time and the speed of light, the inner ring can be measured at 1.37 light years in diameter.

Additionally, the aspect of the ring in relationship the the earth is tilted. The top of the ring is closer to the earth than the bottom. While the entire ring was lit at the same time since SN 1987 A is at the center, it did not appear so from earth. The top of the ring was lit first and the light proceeded around the star until the ring was closed at the bottom. This was caused by the increased distance that the light from the bottom of the ring had to travel to reach earth. This time was measured and, since the speed of light is known, the diameter of the ring can be calculated. It is calculated to be 1.37 light years.

The distance to SN 1987 A can be easily calculated trigonometrically. The angular size of the ring as seen in a telescope tells us that SN 1987 A and the Large Magellanic Cloud are 170,000 light years away.

It seems that creationist arguments for a young earth based on unsupported assertions for a change in the speed of light have been falsified. This same observation falsifies creationist assertions that the rate of radioactive decay has changed. If one changes, the other must necessarily change. Therefore, challenges to radiometric dating must be based on other arguments. Interestingly, there are not other arguments against isochron dating.

Apparently the earth is old and the universe is even older."

Parts of the preceding were originally excerpted from the following WWW sites:

http://www.infidels.org/library/modern/dave_matson/young-earth/additional_topics/supernova.html

http://www.geocities.com/Athens/Thebes/7755/ancientproof/SN1987A.html (not active)
Additional Information:

The Decay of c-decay: http://www.talkorigins.org/faqs/c-decay.html

The Bayou C57/56 observation: http://home.houston.rr.com/bybayouu/SN1987A.htm (not active)

Last Updated: 02/17/2016