Were Adam and Eve Toast?
by Joe Meert
(created 1996, Updated January 2001)
One of the issues in the creation/evolution debate is the
claim that radioactive decay is not constant. In order for the Earth to appear
old, creationists must assume that radioactive decay rates in the past were
faster. This solves the problems of old ages in rocks, but unfortunately opens
up a bigger problem. Radioactive decay gives off heat. The amount of heat
generated is proportional to the rate of decay and the amount of radioactive
material present at the time. In the following exercise, I show how much heat
can be generated by radioactive decay IF decay rates were faster in the past.
Please note that the following analysis uses present-day heat production values
which are observable quantities and I have also assumed (in the creationist
analysis) that each of the elements has the same rate of decay. Changing
the decay rates to those observed today for each of the major heat producing
elements makes the mathematics a bit more tedious, but does not significantly
alter the conclusions given here.
Present day of heat production from radioactive decay in the Earth is produced
mainly by the isotopes 238U, 235U, 232Th and 40K
and has a value of 6.18 x 10-12 W/kg (Turcotte and Schubert, 1982).
If the heat flow out of the Earth were due solely to radioactive decay in the
mantle and crust, it would equal:
Heat Production * Mass of Mantle + Crust
6.18 x 10-12 W/kg * 4.0 x 1024 Kg
= 2.47 x 1013 W
(Eqn 1)
the heat flow out of the Earth can be calculated from
Fourier's Law of heat conduction:
Q = k dt/dz, where:
k = thermal conductivity of
the rocks W/m oC
dt/dz = geothermal gradient
(change in temp with depth)
Q= W/m2
To calculate the surface heat flow, we divide the result
from Eqn 1 by the total surface area of the earth (5.1 x 1014
m2)
2.47 x 1013 W / 5.1 x 1014 m2
= .048 W/m2
(Eqn 2)
If we now use this to calculate the temperature-depth
profile dt/dz, we need to use an average value of thermal conductivity. I
use 3.00 W/m oC as an average thermal conductivity of the rocks.
This yields:
dt/dz =
.048 W/m2 / 3 W/m oC = 16 oC/km
(Eqn 3)
Thus, for every 1 kilometer depth, the temperature will
increase by about 16 oC.
Special Note: As you get deeper into the crust and mantle, temperature increases
are not linear because they are a function of pressure and other factors.
Nevertheless, this relationship is useful to depths of 30-70 kilometers.
Therefore, at a depth of 10 kilometers, the temperature would be about 160 oC.
Basaltic rock melts at about 1200 oC.
Let's look at these same relationships with a much younger earth and a faster
rate of decay. In my example, I will use a 'standard' creationist age for
the earth of 6000 years. In order to carry out the analysis, we must still
assume some sort of decay 'constant'. There are a number of ways this
could be done, but the simplest is to assign an average half-life. I will
use 500 years as the average ½ life for the radioactive elements listed above.
In reality, I am being OVERLY generous to the young Earth crowd. If rates
were variable, they would probably have been much faster than this and the
resultant earth conditions would be more extreme. The interested reader
can easily play with the variables on a spreadsheet and see how they affect the
conclusions reached below.
In order to figure out the rate of heat production in
the past, we must first calculate a decay constant lambda (l).
This is calculated from
t ½ = ln 2 / l
or l = ln
2 / t ½
using 500 years for t ½ , we get l
= 1.38 x 10-3.
The rate of heat production at any time in the past is
given by the following formula (Turcotte and Schubert, 1982):
Hpast = Hpresent
* e l (t-t0)
we use Hpresent
= 6.18 x 10-12
W/kg.
and t-t0= 6000 years and l
as calculated above and we get:
Hpast = 2.43
x 10-8 W/kg
We can now use this value to calculate the amount of heat
flow out of the Earth due solely to this ancient (6000 year old) heat production
and calculate a thermal profile as we did above in Eqn 1 and 2.
Hpast * Mass of Mantle + crust =
total heat production
Hpast = 2.43 x 10-8 W/kg * 4.0 x 1024
kg = 9.75 x 1016 W
We now divide this value by the surface area of the Earth
to get the heat flow Q at 6000 years ago.
Q = 9.75
x 1016 W / 5.1 x 1014 m2 =
191 W/m2
Using the same value for thermal conductivity 3.00 W/m
oC, we can calculate the dt/dz profile as above in Eqn 3:
191 W/m2 / 3.00 W/ m oC = 70,000
oC/ km!!
At 6000 years ago, it is pretty obvious
that the entire Earth would be molten and Adam and Eve's goose was cooked.
I must also add that because of these extreme temperatures, a purely conductive
heat regime is implausible. I am not implying that
this is a purely conductive regime. What I am showing is that the thermal regime
on a 6000 year old earth with rampant radioactive decay is extreme. If you want
to turn off the engine and let the Earth cool from this extreme you also run
into time spans much greater than 6000 years because it will take a while to
cool down from those extreme temperatures. It's difficult to estimate how long
it would take for the Earth to reach present-day temperatures because I frankly
don't know where the creationists would take their argument. It is clear that
rapid decay results in a tremendous release of heat. I suppose you could always
argue that the Earth has been cooling since this initial heating and that there
is no further significant heat released by radioactive decay. In that case, the
cooling of the Earth reduces to the Kelvin problem and gives an age of 20-60
million years. The graph below gives some of the major events in
Creationist history along with the geothermal gradient.
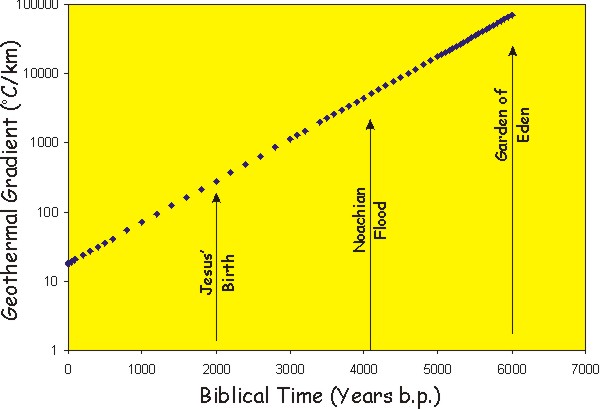
Note the Scale is semi-logarithmic.
Additional Notes/Updates
(a) I did a rough calculation for the Earth's conductive profile using the old
Earth model and the average geothermal gradient 3.5 billion years ago is about
27 oC/km.
(b) Just for those who are interested, if Noah's flood took place about 4000
years ago, this calculation yields roughly 40,000 oC/km. Guess what?
Maybe there was a vapor canopy anyway since liquid water would not be present!!
(c) At the time of Jesus' birth, the geothermal
gradient would have been ~400 oC/km.
Note: Several creationists have commented that the
calculations would not be correct if the speed of light has decayed over the
past 6000 years. This is due to the fact that the speed of light factors
into radioactive decay equations/energy. At present, there is no evidence
to suggest that the speed of light (in vacuo) is a variable.
Until such a time when this assertion can be
substantiated with real data, the argument stands testament to one of the major
problems associated with rapid decay proposals. In fact, 'creation
scientists' at the Institute
for Creation Research have noted:
"One major obstacle to accelerated decay is an
explanation for the disposal of the great quantities of heat which would be
generated by radioactive decay over short periods of time. For example, if
most of the radioactive decay implied by fission tracks or quantities of
daughter products occurred over the year of the Flood, the amount of heat
generated would have been excessive, given present conditions."
Refs: 1. Turcotte & Schubert, 1982, Geodynamics,
John Wiley and Sons
OTHER ON-LINE ARTICLES ON
YE-CREATIONISM by Joe Meert

