Creationists promote the falsehood that the second law of thermodynamics does not permit entropy to spontaneously decrease, and therefore evolution could not have happened. According to creationists, entropy can only increase, resulting in a "universal decay" of any and all systems. However, the mathematical laws of thermodynamics make it perfectly clear: it is possible for the entropy of a system to spontaneously decrease, providing the over-all entropy of the system's surroundings increases to a greater degree.
Thermodynamics deals in a quantitative manner with the relationship between heat and work. Because of this, its known applications must necessarily be limited to man-made devices and chemical changes for which heat and work parameters can be established. These parameters have been established for a number of biochemical reactions, but this information has not resulted in the general ability to determine the thermodynamics of cell growth in living organisms. Creationists take advantage of this situation by postulating a pseudo science explanation for the obvious flaw in their argument: if all systems can only go in the direction of universal decay, then how can one explain the growth of living things, which is just the opposite of universal decay? Creationist propaganda postulates, with no scientific justification whatever, an "energy conversion mechanism" for living things that "overcomes" the laws of thermodynamics. However, in the case of the evolution of living things, this "energy conversion mechanism" is strangely absent!
The controversy can be summed up as follows:
Creationist: The second law of thermodynamics states that entropy can only increase, resulting in a universal decay of all systems.
Evolutionist: But the mathematical laws of thermodynamics state very clearly that entropy can spontaneously decrease!
Creationist: Well, that is technically true for inorganic systems, but it doesn't apply to living systems.
Evolutionist: So you're saying that entropy can not spontaneously decrease for living systems? Doesn't that mean that living things can only undergo universal decay? How then do you explain the fact they grow and reproduce?
Creationist: Well, we believe that there is a special "energy conversion mechanism" that allows living systems to overcome the laws of thermodynamics.
Evolutionist: First you said the laws of thermodynamics were universal, and now you say they are not. Please explain the discrepancy.
Creationist: God can do anything He pleases.
Creationists believe that the second law of thermodynamics does not permit order to arise from disorder, and therefore the macro evolution of complex living things from single-celled ancestors could not have occurred. The creationist argument is based on their interpretation of the relationship between probability and a thermodynamic property called "entropy."
By way of background, and in order to clarify the creationist position, let me quote from the creationist literature:
The Remarkable Birth of Planet Earth, by Henry Morris:
(p. 14) All processes manifest a tendency toward decay and disintegration,
with a net increase in what is called the entropy, or state of randomness or
disorder, of the system. This is called the Second Law of
Thermodynamics.
(p. 19) There is a universal tendency for all systems to go from
order to
disorder, as stated in the Second Law, and this tendency can only be arrested
and reversed under very special circumstances. We have already seen, in
Chapter I, that disorder can never produce order through any kind of random
process. There must be present some form of code or program, to direct the
ordering process, and this code must contain at least as much
"information" as is needed to provide this direction.
Furthermore,
there must be present some kind of mechanism for converting the environmental
energy into the energy required to produce the higher organization of the
system involved. ...
Thus, any system that experiences even a temporary
growth
in order and complexity must not only be "open" to the sun's energy
but must also contain a "program" to direct the growth and a
"mechanism" to energize the growth.
Scientific Creationism, edited by Henry Morris:
(p.25) The Second Law (Law of Energy Decay) states that every system
left to its own devices always tends to move from order to disorder, its
energy tending to be transformed into lower levels of availability, finally
reaching the state of complete randomness and unavailability for further
work.
Of course, the creationist application of the second law of thermodynamics to the development of living things is inconsistent with any model of origins. Creationists get around this problem by invoking the supernatural:
The Genesis Flood, by Whitcomb and Morris:
(p. 223) But during the period of Creation, God was introducing order and
organization into the universe in a very high degree, even to life itself!
It is thus quite plain that the processes used by God in creation were
utterly different from the processes which now operate in the universe!
As will be shown later on, it is only the over-all entropy of a complete, or closed system that must increase when spontaneous change occurs. In the case of spontaneously interacting sub-systems of a closed system, some may gain entropy, while others may lose entropy. For example, it is a fundamental axiom of thermodynamics that when heat flows from subsystem A to subsystem B, the entropy of A decreases and the entropy of B increases. The statement that an increase in order can only occur as the result of a directional mechanism, program, or code is misleading. Any process that can be demonstrated to take place with an increase in order/decrease in entropy is arbitrarily deemed to be the consequence of an undefined "directional mechanism."
Probability, as used in thermodynamics, means the probability that some specific change will occur. Probability is related to the thermodynamic concept of irreversibility. An irreversible physical or chemical change is a change that will not spontaneously reverse itself without some change in the surrounding conditions. Irreversible changes have a high degree of probability. The probability of an irreversible change spontaneously reversing itself without outside interference is zero.
When we say that a change is irreversible (in the thermodynamics sense) it means only that the change will not spontaneously reverse itself without some change in the surrounding conditions. It does not mean that it cannot be reversed by any means at all!
It is important to remember that a change that has a high degree of probability under one set of circumstances may have a very low degree of probability under a different set of circumstances. To illustrate: If the temperature drops below freezing, the probability of water becoming ice is very high. The change from water to ice is thermodynamically irreversible. If the surrounding temperature should happen to rise above the freezing point, the probability of water becoming ice, or remaining as ice, is zero. Under these conditions the reverse change of ice to liquid water is also thermodynamically irreversible.
Failure to understand that in thermodynamics probabilities are not fixed entities has led to a misinterpretation that is responsible for the wide- spread and totally false belief that the second law of thermodynamics does not permit order to spontaneously arise from disorder. In fact, there are many examples in nature where order does arise spontaneously from disorder: Snowflakes with their six-sided crystalline symmetry are formed spontaneously from randomly moving water vapor molecules. Salts with precise planes of crystalline symmetry form spontaneously when water evaporates from a solution. Seeds sprout into flowering plants and eggs develop into chicks.
Thermodynamics is an exact science that is based on a limited number of specific mathematical concepts. It is not explainable in terms of qualitative metaphors. In order to understand the relationship between probability and the second law, the reader must be familiar with the relationship between probability and entropy. Entropy is a mathematically defined entity which is the fundamental basis of the second law of thermodynamics and all of its engineering and physical chemistry ramifications.
In the following sections we will try to explain the true relation between entropy and probability and show why this relationship does not preclude the possibility of order spontaneously arising from disorder.
In describing the laws of thermodynamics we often refer to "systems." A system is a specific entity or object or region in space to be evaluated in terms of its thermodynamic properties and possible changes. It could be an ice cube, a toy balloon, a steam turbine, or even the entire earth itself.
The concept of entropy is fundamental to understanding the second law of thermodynamics. Entropy (or more specifically, increase in entropy) is defined as heat (in calories or Btu's) absorbed by a system, divided by the absolute temperature of the system at the time the heat is absorbed. Absolute temperature is the number of degrees above "absolute zero", the coldest temperature that can exist.
The total entropy in a system is represented by the symbol S. The symbol
![]() S is used to represent a given change in the entropy content of a system.
If the symbol q is used to represent the amount of heat absorbed by a system,
the equation for the resulting entropy increase is:
S is used to represent a given change in the entropy content of a system.
If the symbol q is used to represent the amount of heat absorbed by a system,
the equation for the resulting entropy increase is:
 S = q/T (1)
S = q/T (1)
Where T is the absolute temperature.
When heat is absorbed, the entropy of a system increases; when heat flows out of
a system, its entropy decreases.
The "surroundings" of a system is everything outside of the system that can interact with it; surroundings can usually be defined as the space that surrounds a system. When heat is evolved by a system, that same heat is absorbed by its surroundings. When heat is absorbed by a system, that same heat must necessarily come from its surroundings. Therefore any entropy increase in a system due to heat flow must be accompanied by an entropy decrease in the surroundings, and vice versa.
When heat flows spontaneously from a hotter region to a cooler region, the entropy decrease in the hotter region will always be less than the entropy increase in the cooler region, because the greater the absolute temperature, the smaller the entropy change for any particular heat flow. (See equation 1, above)As an example, consider the entropy change when a large rock at 500 degrees absolute is dropped into water at 650 degrees absolute. (We are using an absolute temperature scale based on Fahrenheit degrees; on this scale, water freezes at 492 degrees.) For each Btu of heat that flows into the rock at these temperatures the entropy increase in the rock is 1/500 = 0.0020 and the entropy decrease of the water is 1/650 = 0.0015. The difference between these values is 0.0020 - 0.0015 = 0.0005. This represents the over all entropy increase of the system (rock) and its surroundings (water).
Of course the rock will warm up to, and the water cool to, a temperature intermediate between their original temperatures, thus considerably complicating the calculation of total entropy change after equilibrium is achieved. Nevertheless, for every Btu of heat transferred from water to rock there will always be an increase of over-all net entropy.
As was mentioned before, a spontaneous change is an irreversible change. Therefore an increase in the overall net entropy can be used as a measure of the irreversibility of spontaneous heat flow.
Irreversible changes in a system can, and often do, take place even though there may be no interaction, and negligible heat flow, between system and surroundings. In cases like these the entropy "content" of the system is greater after the change than before. Even when heat flow does not occur between system and surroundings, spontaneous changes inside an isolated system are always accompanied by an increase in the system's entropy, and this calculated entropy increase can be used as a measure of irreversibility. The following paragraphs will explain how this entropy increase can, at least in some cases, be calculated.
It is an axiom of thermodynamics that entropy, like temperature, pressure, density, etc., is a property of a system and depends only on the existing condition of the system. Regardless of the procedures followed in achieving a given condition, the entropy content for that condition is always the same. In other words, for any given set of values for pressure, temperature, density, composition, etc., there can be only one value for the entropy content. It is essential to remember this: When a system that has undergone an irreversible change is restored to its original condition (same temperature, pressure, volume, etc.) its entropy content will likewise be the same as it was before.
In cases where an isolated system undergoes an entropy increase as the result
of a spontaneous change inside the system, we can calculate that entropy
increase by postulating a procedure whereby the system's entropy increase is
transferred to the surroundings in a manner such that there is no further
increase in net entropy and the system is restored to its original
condition.
The entropy increase of the surroundings can then be readily calculated by
equation (1): ![]() S = q/T, where q = heat absorbed by the
surroundings, and
T = absolute temperature of the surroundings.
S = q/T, where q = heat absorbed by the
surroundings, and
T = absolute temperature of the surroundings.
It bears repeating that when the system is restored to its original condition, its entropy content will be the same as it was before its irreversible change. Therefore the amount of entropy absorbed by the surroundings during restoration must necessarily be the same as the entropy increase accompanying the system's original irreversible change, providing that there is no further increase in net entropy during restoration.
This postulated restoration procedure and the postulated properties of the surroundings are for the purpose of calculation only. Since we are not dealing with the surroundings as such, they can be postulated in whatever form necessary to simplify the calculations; it is neither necessary nor desirable that the surroundings correspond to any condition that could actually exist. Therefore, we will postulate a theoretical restoration procedure that takes place with no further increase in net entropy, even though such a procedure can not actually be obtained experimentally.
The restoration process, if it were to take place in actuality, would have to be accompanied by at least a small amount of irreversibility, and hence an additional increase in the entropy of the surroundings beyond the entropy increase from the system's original irreversible change. This is because heat will not flow without a temperature differential, friction cannot be entirely eliminated, etc. Therefore the restoring process, if it is to take place with no further increase in over-all net entropy, must be postulated to take place with no irreversibility. If such a process could be actually realized, it would be characterized by a continuous state of equilibrium (i.e. no pressure or temperature differentials) and would occur at a rate so slow as to require infinite time. Processes like these are called "reversible" processes. Remember, reversible processes are postulated to simplify the calculation of the entropy change in a system; it is not necessary that they be capable of being achieved experimentally.
It should not be assumed that equation (1) requires that q, the heat absorbed, must necessarily be absorbed reversibly. The concept of reversibility is merely a means to an end: the calculation of entropy change accompanying an irreversible process.
The following example will illustrate the calculation of a reversible restoring process and at the same time develop the equation which is the basis for the thermodynamical relationship between probability and the second law.
An "ideal" gas is one in which the distribution of molecules is dependent on probability only; other factors, like intermolecular forces, are considered to non existent. Therefore the mathematical equations dealing with an ideal gas can be used as a basis for the purpose of calculating the relationship between probability and entropy. In practice, no gas is completely ideal, and the ideal gas law equations must be modified to take this into account. But in the following calculations, we are dealing with the ideal gas law mathematics as a probability of distribution model only, in order to facilitate the determination of the entropy-probability relationship.
We will postulate a system consisting of an ideal gas contained in a tank connected to a second tank that has been completely evacuated, with the valve between the two tanks closed. The temperature of the system and its surroundings is postulated to be the same. It bears repeating: We are not dealing with an actual experiment. We are dealing with a probability distribution determination taking place under conditions that permit the calculation of the basic entropy-probability equation.
When the valve is opened the gas expands irreversibly from V1 (its original volume) to V2 (the volume of both tanks). There is no work of compression by or upon the surroundings. Because the gas is ideal there is no temperature change, and hence no heat flow takes place.
After expanding irreversibly from V1 to V2, the gas is restored to its original condition by reversibly compressing it back to V1. This compression requires work (force applied through a distance) which in turn generates heat in the gas, heat that is absorbed by the surroundings so that there is no increase in the gas temperature. In our mathematical model of this reversible restoring process, the surroundings are postulated to be so large that they also do not undergo any temperature increase. The temperature T remains unchanged during the entire irreversible expansion and subsequent reversible restoration process.
The work of compressing the gas during restoration is equal to the pressure
of the gas times the volume change due to compression. Because the pressure
increases during compression, the work of compression must be determined by
the calculus equation:
compression work =The integral signPdV where: P = pressure V = volume dV = the small change in volume corresponding to pressure P
The equation relating temperature, pressure, and volume of an ideal gas is:
PV = RT (2) where: P = pressure
V = volume
T = absolute temperature
R = a constant which depends only on the amount of gas present
In the case of a reversible, isothermal compression of an ideal gas we may
substitute P from equation (2) into the equation for compression work. When
this is done, we have:
compression work = RTdV/V (3)
Although it is not necessary that our postulated reversible restoration process be capable of being carried out in a practical sense, it is nevertheless sometimes helpful to be able to visualize the process. To this end, the reader may consider the restoring compression process being brought about by a piston fitted into the end of the second tank. On compression from V2 to V1, the piston moves down the length of the second tank, and with no mechanical friction forces all the gas contained therein back into the first tank V1.
Since the work of compression is equal to q, the heat absorbed by the surroundings, q may be substituted in equation (3) to give:
q = RTFrom equation (1) the entropy gained by the surroundings during restoration from V2 to V1 is:dV/V (4)
Substituting from equation (4):S = q/T (1)
S = R
dV/V
Upon integrating (a calculus procedure for summing up the individual values of dV/V) we have:
Where ln(V2/V1) is the natural logarithm of the ratio of expanded volume to the initial volume, andS = Rln(V2/V1) (5)
The ratio of the probability that all the gas molecules are evenly distributed between the two tanks to the probability that all the molecules, of their own accord and by random motion, would be in tank V1 is equal to (V2/V1)N, where N is the number of molecules.
If V2/V1 were equal to 2.0, for example, and N were equal to 10, the probability ratio would be 2 to the tenth power, or 1024. For N = 100, the ratio would be approximately 1.27 times ten to the 30th power. It is clear that the random motion of trillions of gas molecules heavily favors a uniform distribution.
let X1 = the probability of all the gas molecules, after the valve is
opened, remaining in the first tank V1
let X2 = the probability of all the gas molecules, after the valve is
opened, being uniformly distributed in V2, the volume of both
tanks.
From the probability equation, we have:
X2/X1 = (V2/V1)N.
Taking the natural logarithm of both sides, and then multiplying both sides
by R, the gas constant:
R ln(X2/X1) = RN ln(V2/V1) R/N ln(X2/X1) = R ln(V2/V1)Substituting in equation (5):
S = R/N ln(X2/X1) (6)
Equation (6) represents the fundamental relationship between probability and the second law of thermodynamics. It states that the entropy of our ideal gas model increases when its molecular distribution changes from a lower probability to a higher probability (X2 greater than X1).
For the general case, equation (6) can be written:Where K is a constant depending on the particular change involved.S = K ln(X2/X1) (7)
However, equation (7) is not particularly useful in predicting whether or not a given chemical change can take place. We can assume that it applies to all systems, not just gaseous, but not knowing the value of K and the probability of existence of each of the interacting compounds make its use impractical. The problem is solved by determining the change in a thermodynamic property called the "free energy," designated by ![]() F. The mathematics used in deriving and using
F. The mathematics used in deriving and using ![]() F are complex, extensive, and beyond the scope of an explanation designed for the lay person. For those interested in further research on the subject, Thermodynamics, by Lewis and Randall, revised by Pitzer and Brewer, is a good source.
F are complex, extensive, and beyond the scope of an explanation designed for the lay person. For those interested in further research on the subject, Thermodynamics, by Lewis and Randall, revised by Pitzer and Brewer, is a good source. ![]() F represents the energy available to do useful work as a result of a chemical change. If a chemical change can take place,
F represents the energy available to do useful work as a result of a chemical change. If a chemical change can take place, ![]() F for the change is negative, indicating that the free energy content of the reactants is reduced in forming the products.
F for the change is negative, indicating that the free energy content of the reactants is reduced in forming the products. ![]() F is not the same as the heat evolved in a chemical change. Some spontaneous reactions actually absorb heat as they proceed. An example would be chemically activated cold packs. Many factors can change
F is not the same as the heat evolved in a chemical change. Some spontaneous reactions actually absorb heat as they proceed. An example would be chemically activated cold packs. Many factors can change ![]() F for a given chemical change, not the least of which are temperature and a change in the other inter-reacting compounds. Also, some reactions with a negative
F for a given chemical change, not the least of which are temperature and a change in the other inter-reacting compounds. Also, some reactions with a negative ![]() F will not proceed without a catalyst. An example is the combination of hydrogen and oxygen at room temperature. A mathematical definition of the free energy change is:
F will not proceed without a catalyst. An example is the combination of hydrogen and oxygen at room temperature. A mathematical definition of the free energy change is:
![]() F =
F = ![]() H - T
H - T![]() S
S
Where ![]() H is the constant pressure calorimeter heat evolved when the reaction takes place.
H is the constant pressure calorimeter heat evolved when the reaction takes place.
Returning to the relationship between entropy and probability, keeping in mind its practical limitations in determining whether or not a given reaction can proceed:
As we have seen before, ![]() S can be either positive or negative.
When
S can be either positive or negative.
When ![]() S is negative equation (7) can be written:
S is negative equation (7) can be written:
-Therefore a system can go from a more probable state (X2) to a less probable state (X1), providingS = -K ln(X2/X1) = K ln(X1/X2)
In the case of the formation of the complex molecules characteristic of living organisms, creationists raise the point that when living things decay after death, the process of decay takes place with an increase in entropy. They also point out, correctly, that a spontaneous change in a system takes place with a high degree of probability. They fail to realize, however, that probability is relative, and a spontaneous change in a system can be reversed, providing the system interacts with its surroundings in such a manner that the entropy increase in the surroundings is more than enough to reverse the system's original entropy increase.
The application of energy can reverse a spontaneous, thermodynamically "irreversible" reaction. Leaves will spontaneously burn (combine with oxygen) to form water and carbon dioxide. The sun's energy, through the process of photosynthesis, will produce leaves from water vapor and carbon dioxide, and form oxygen.
If we unplug a refrigerator, heat will flow to the interior from the surroundings; the entropy increase inside the refrigerator will be greater than the entropy decrease in the surroundings, and the net entropy change is positive. If we plug it in, this spontaneous "irreversible" change is reversed. Due to the input of electrical energy to the compressor, the heat transferred to the surroundings from the condenser coils is greater than the heat extracted from the refrigerator, and the entropy increase of the surroundings is greater than the entropy decrease of the interior, in spite of the fact that the surroundings are at a higher temperature. Here again, the net entropy change is positive, as would be expected for any spontaneous process.
In a similar manner, the application of electrical energy can reverse the spontaneous reaction of hydrogen and oxygen to form water: when a current is passed through a water solution, hydrogen is liberated at one electrode, oxygen at the other.
As can easily be confirmed experimentally, agitating water raises its temperature. When water falls freely from a higher elevation to a lower elevation, its energy is changed from potential to kinetic, and finally to heat as it splashes at the end of its fall. The second law of thermo- dynamics states that the water will not spontaneously raise itself to its original elevation using the heat produced on splashing as the sole source of energy. To do so would require a heat engine that would convert all of the heat of splashing to mechanical energy.
The efficiency of a heat engine is thermodynamically limited by the Carnot
cycle, which limits the efficiency of any heat engine to ![]() T/T, where
T/T, where
![]() T is the temperature increase due to splashing, and T is
the absolute
temperature. Since
T is the temperature increase due to splashing, and T is
the absolute
temperature. Since ![]() T is only a small fraction of T,
there is no device that
could be constructed which would allow all of the water to spontaneously jump
back to its former elevation.
T is only a small fraction of T,
there is no device that
could be constructed which would allow all of the water to spontaneously jump
back to its former elevation.
We can, at least in theory, calculate the entropy increase of the water resulting from its irreversible change in falling. In a manner analogous to that used in the previous example, the entropy increase would be equal to the heat generated by splashing agitation, divided by the absolute temperature. If some of the energy of the falling water is extracted by a water wheel, there will be less heat of splashing and hence less entropy increase. A properly designed turbine could extract most of the water's kinetic energy. This is not the same thing as trying to utilize the heat of splashing as an energy source for a heat engine to raise the water. In other words, using the energy before it becomes heat is much more efficient than trying to use it after it becomes heat.
If a water wheel is connected by shafts, belts, pulleys, etc. to a pump, the pump can raise water from the downstream side of the water wheel to an elevation even higher than that of the upstream reservoir. Some of the water would spontaneously raise itself to an elevation even higher than original, but the rest of it would end up below the water wheel on the downstream side.
While it is not possible for all of the water to raise itself to an elevation higher than its initial elevation, it is possible for some of the water to spontaneously raise itself to an elevation higher than initial. As with any other irreversible change, there will be an increase in over-all entropy. This means that the entropy increase of the water going over the wheel is greater than the entropy decrease of water pumped up to the higher elevation.
This will be confirmed mathematically in the following paragraphs.
![]() will stand for the Greek letter gamma, representing unit weight
in pounds per cubic foot. An increase in the value of a parameter
will be represented by
will stand for the Greek letter gamma, representing unit weight
in pounds per cubic foot. An increase in the value of a parameter
will be represented by ![]() .
.
Let: 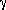 = unit weight of water, lbs./cubic foot
h = height of reservoir above downstream side, feet
= unit weight of water, lbs./cubic foot
h = height of reservoir above downstream side, feet
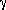 h = potential energy of water in reservoir
h = potential energy of water in reservoir
 h = additional height above reservoir (to which water is pumped)
h +
h = additional height above reservoir (to which water is pumped)
h +  h = height to which water is pumped, feet above downstream side
w = work of pumping water to higher elevation
q = heat loss due to pump friction and downstream agitation
f = fraction of water pumped to elevation h +
h = height to which water is pumped, feet above downstream side
w = work of pumping water to higher elevation
q = heat loss due to pump friction and downstream agitation
f = fraction of water pumped to elevation h +  h
From the flow equation, energy in = energy out:
h
From the flow equation, energy in = energy out:
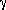 h = q + w (8)
Where:
h = q + w (8)
Where: 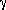 h is the total energy expended by the water
in falling from height h. q = the energy wasted as heat of splashing,
and w = work expended in pumping the water to a higher elevation.
q = T
h is the total energy expended by the water
in falling from height h. q = the energy wasted as heat of splashing,
and w = work expended in pumping the water to a higher elevation.
q = T S (equation 1)
w = f
S (equation 1)
w = f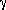 (h +
(h +  h)
The total energy available,
h)
The total energy available, 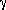 h, is divided into pump
work, f
h, is divided into pump
work, f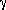 (h +
(h +  h), and energy
lost, T
h), and energy
lost, T S:
S:
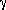 h = T
h = T S + f
S + f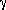 (h +
(h +  h)
Rearranging:
T
h)
Rearranging:
T S =
S = 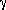 h - f
h - f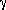 (h +
(h +  h) (8)
When no pump work is done, then:
T
h) (8)
When no pump work is done, then:
T S' =
S' = 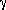 h (9)
Combining equations (8) and (9), we get:
h (9)
Combining equations (8) and (9), we get:
 S' -
S' -  S = f
S = f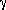 (h +
(h +  h)/T (10)
h)/T (10)
In the case where the water falls freely without turning the water wheel or
operating the pump:
let q'= heat of splashing
q'= T S',
where
S',
where  S' is the entropy increase on free fall
S' is the entropy increase on free fall
Equation (10) shows that Equation (10) also shows that the lower the value of ![]() S, the more efficient
the pump, and the greater the value of f, the fraction of water pumped.
S, the more efficient
the pump, and the greater the value of f, the fraction of water pumped.
Creationists assume that a change characterized by a decrease in entropy can not occur under any circumstances. In fact, spontaneous entropy decreases can, and do, occur all the time, providing sufficient energy is available. The fact that the water wheel and pump are man-built contraptions has no bearing on the case: thermodynamics does not concern itself with the detailed description of a system; it deals only with the relationship between initial and final states of a given system (in this case, the water wheel and pump).
A favorite argument of creationists is that the probability of evolution occurring is about the same as the probability that a tornado blowing through a junkyard could form an airplane. They base this argument on their belief that changes in living things have a very low probability and could not occur without "intelligent design" which overcomes the laws of thermodynamics. This represents a fundamental contradiction in which (they say) evolution is inconsistent with thermodynamics because thermodynamics doesn't permit order to spontaneously arise from disorder, but creationism (in the guise of intelligent design) doesn't have to be consistent with the laws of thermodynamics.
A simpler analogy to the airplane/junkyard scenario would be the stacking of three blocks neatly on top of each other. To do this, intelligent design is required, but stacking does not violate the laws of thermodynamics. The same relations hold for this activity as for any other activity involving thermodynamical energy changes. It is true that the blocks will not stack themselves, but as far as thermodynamics is concerned, all that is required is the energy to pick them up and place them one on top of the other. Thermodynamics merely correlates the energy relationships in going from state A to state B. If the energy relationships permit, the change may occur. If they don't permit it, the change can not occur. A ball will not spontaneously leap up from the floor, but if it is dropped, it will spontaneously bounce up from the floor. If sufficient energy is available, the ball will spontaneously "leap" from the floor.
Considering the earth as a system, any change that is accompanied by an entropy decrease (and hence going back from higher probability to lower probability) is possible as long as sufficient energy is available. The ultimate source of most of that energy, is of course, the sun. The numerical calculation of entropy changes accompanying physical and chemical changes are very well understood and are the basis of the mathematical determination of free energy, emf characteristics of voltaic cells, equilibrium constants, refrigeration cycles, steam turbine operating parameters, and a host of other parameters. The creationist position would necessarily discard the entire mathematical framework of thermodynamics and would provide no basis for the engineering design of turbines, refrigeration units, industrial pumps, etc. It would do away with the well-developed mathematical relationships of physical chemistry, including the effect of temperature and pressure on equilibrium constants and phase changes.
Copyright 1995 Frank Steiger. This document may be reproduced without royalty for non-profit, non-commercial use.